Il y a quelques temps, une connaissance, perplexe, m’avait partagé la vidéo suivante (elle diffuse deux fois de suite la même démonstration) :
Vous l’avez remarqué : le chocolat a perdu un carré, mais il semble ne pas avoir changé de volume. Comment, selon vous, ce « miracle » s’est-il produit? Vous donnez votre langue au chat? Pas de panique! Voici quelques explications.
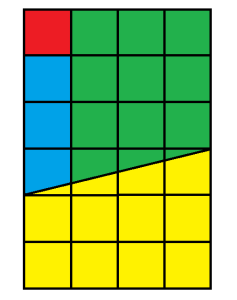
Au commencement, il y a une tablette de chocolat.
Ensuite on découpe le chocolat comme montré dans la vidéo.
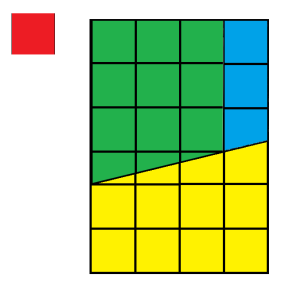
En déplaçant les blocs, on obtient la tablette de chocolat moins le petit carré rouge.
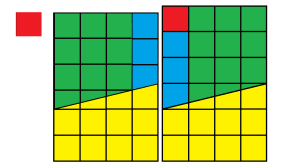
Nous avons, au final, une tablette de chocolat. Mais, en le regardant bien, il semble que les pièces près de la diagonale ne collent pas tout à fait ensemble. Ceci est du à la perte de volume (le carré rouge a été enlevé). (C’est quelque chose qu’on remarque un peu moins pour un chocolat à une seule couleur, ce qui est le cas de pas mal de chocolat bien entendu.) D’ailleurs, si nous comparons ce chocolat ci-dessus avec le chocolat de la Figure 2, nous obtenons l’image suivante :
Le chocolat de gauche est plus petit en hauteur que le chocolat de droite. Donc, il y a bel et bien eu perte de volume, et ce volume vaut celui du petit carré rouge.
Le rêve de produire du chocolat à l’infini n’est donc qu’une chimère (dommage!). Au moins, cette vidéo est une belle illustration de la géométrie (et de la gourmandise).
Parenthèse : un peu de maths
La démonstration est finie, mais, pour ceux et celles qui s’intéressent plus à l’aspect mathématique des choses, en voici une démonstration algébrique.
Soit ![]() la longueur du côté du petit carré rouge. Le chocolat a donc une longueur de
la longueur du côté du petit carré rouge. Le chocolat a donc une longueur de ![]() et une largeur de
et une largeur de ![]() . L’aire du carré rouge vaut donc
. L’aire du carré rouge vaut donc ![]() , et, avec un peu de calcul, on déduit que l’aire jaune vaut
, et, avec un peu de calcul, on déduit que l’aire jaune vaut ![]() , l’aire verte
, l’aire verte ![]() et l’aire bleue
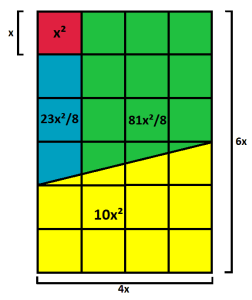
et l’aire bleue ![]() . Tout cela est représentée dans la figure suivante.
. Tout cela est représentée dans la figure suivante.
Maintenant, si l’on veut calculer l’aire du volume du chocolat de la Figure 3, il suffit d’additionner les aires jaune, verte et bleue, ce qui donne
![]() .
.
Or, l’aire du chocolat à l’état initial (Figure 1 et 2) est de ![]() . Donc, si l’on soustrait à l’aire du chocolat de la Figure 2, celle de la Figure 3 moins le carré rouge, on obtient
. Donc, si l’on soustrait à l’aire du chocolat de la Figure 2, celle de la Figure 3 moins le carré rouge, on obtient ![]() , ce qui équivaut à l’aire du petit carré rouge.
, ce qui équivaut à l’aire du petit carré rouge.